התקפת sha1 collision

בשבוע האחרון התבשרנו על כך שאלגוריתם הגיבוב SHA-1 נפרץ באופן מעשי. וההשפעה יכולה להיות דרמטית על אפליקציות, אתרים ותוכנות שמשתמשות באלגוריתם הגיבוב הזה. אחת מהן היא Github. אבל יש עוד המון. וההתקפה הזו היא מספיק חשובה כדי לכתוב עליה פה. והיא גם מעניינת.

ראשית, מה זו פונקצית גיבוב? או hash? אני מאמין שרוב המתכנתים מכירים, אבל אם לא – אני אסביר. בגדול זו פונקציה שמקבלת משהו – מחרוזת טקסט, מספר, קובץ, אובייקט, סבתא שלי (טוב, לא סבתא שלי) ומפיקה ממנו מחרוזת טקסט ייחודית שאי אפשר לשחזר ממנה את הטקסט המקורי או האובייקט אבל היא ייחודית (או לפחות אמורה להיות כמעט ייחודית: כלומר אפשר למצוא עוד משהו שיפיק את המחרוזת הזו, אבל זה יקח המון זמן וכוח חישוב). אני חושב שפונקצית הגיבוב הכי מוכרת היום היא MD5 הידועה לשמצה, אבל יש המון.

כאמור יש המון פונקציות גיבוב מסוגים שונים שנבדלים זו מזו בעקרונות המתמטיים המפעילים אותן. זה נשמע מסובך אבל זה לא. נסו בעצמכם! באתר הזה: http://www.sha1-online.com/ אתם יכולים לבדוק את פונקציות הגיבוב השונות. בכללן גם SHA-1. אתם יכולים להקליד את המשפט Hello World ולראות מה פונקציות הגיבוב תפיק. היא תמיד תפיק את מספר הזיהוי המגובב הזה:

0a4d55a8d778e5022fab701977c5d840bbc486d0

זה הכוח של פונקצית גיבוב טובה – היא תמיד תפיק את אותו גיבוב לאותו משפט. אם אני אכניס משפט אחר – היא תפיק לי גיבוב אחר וזהה. נסו בעצמכם ואפשר גם בקוד. כל שפת תכנות תומכת בהשינג (Hashing) ומכילה לא מעט אלגוריתמים. ב-Node.js זה נראה כך:

const crypto = require('crypto');

const hash = crypto.createHash('sha1'); // Creating hash object 
const data = hash.update('Hello World', 'utf-8'); // Passing the data to be hashed
const gen_hash = data.digest('hex'); // Creating the hash in the required format
console.log(`hash : ${gen_hash}`); // hash : 0a4d55a8d778e5022fab701977c5d840bbc486d0

זה כאמור מוכר למדי. אנו משתמשים בגיבוב בהרבה מקומות. למשל כדי לבדוק ייחודיות של טקסטים. תחשבו שיש לי מסמך ארוך ואני רוצה לדעת כמה שורות מתוכו ייחודיות. או ערימה של קבצים שאני רוצה לדעת כמה מהם הם זהים. אבל החשיבות של פונקצית גיבוב היא קריטית בכל מה שקשור לחתימות דיגיטליות ול-https. אני אתמקד בחתימות דיגיטליות. פונקצית גיבוב היא קריטית כדי שנוכל לבדוק שהקובץ שקיבלנו הוא באמת הקובץ שאנו רוצים ולא קובץ עם ׳תוספות׳ שהוזרקו על ידי כל מיני גורמים זדוניים בדרך.

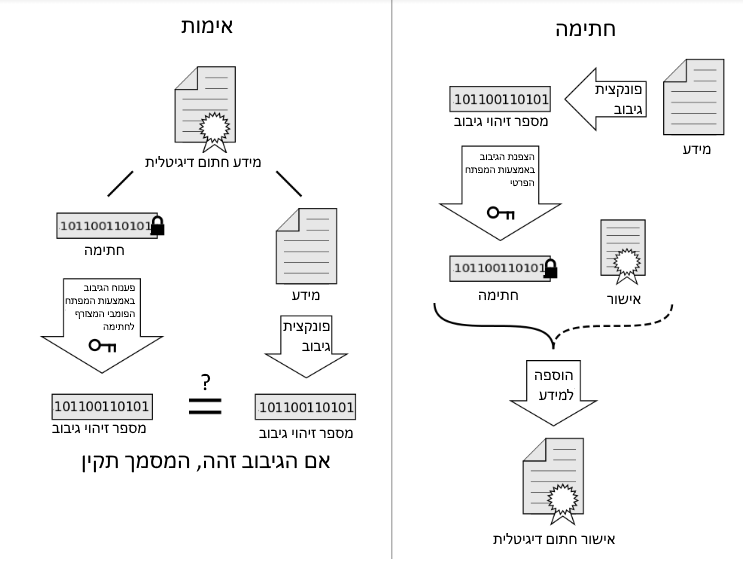
כאשר גורם מסוים רוצה לשלוח קובץ לגורם אחר אבל לא רוצה שמישהו ברשת יוכל לשנות את הקובץ, הוא מבצע תהליך שנקרא ׳חתימה דיגיטלית׳. בבסיס התהליך הזה עומדת פונקצית הגיבוב – שולחים את הקובץ לפונקצית הגיבוב, היא מפיקה מספר מזהה מגובב שזהה וייחודי לאותו קובץ. את המספר הזה מצפינים ושולחים בתעודה. הלקוח, שמקבל את המספר הזה, יכול להכניס את הקובץ שהוא קיבל אל פונקצית הגיבוב כדי לוודא שזה אותו קובץ בדיוק. כאמור בבסיס פונקצית הגיבוב עומדת ההנחה שהיא מספקת ייחודיות – אין שני קבצים (או שתי מחרוזות טקסט) שהן לא ייחודיות. זה בדרך כלל קורה באופן שקוף למשתמש, אבל אפשר לדמות את זה על המחשב.

תבדקו את קובץ ה-PDF הזה למשל. איך בודקים?

אם אתם בלינוקס, פיתחו טרמינל. אם אתם בחלונות, פיתחו את Git bash או כל דמוי Cygwin שיש לכם (אם אתם לא יודעים מה זה Git bash, קראו את המאמר הזה) – מורידים את קובץ ה-PDF לאיזשהו מקום, נכנסים בטרמינל אל המקום שבו הקובץ נמצא ומקלידים:

$ sha1sum shattered-1.pdf

אתם תקבלו את ה-hash. מה הוא?

38762cf7f55934b34d179ae6a4c80cadccbb7f0a

ה-hash הזה אמור להיות ייחודי. הוא חייב להיות ייחודי. למה? כי אם הוא לא יהיה ייחודי, אם כל אחד יוכל לקחת כל מסמך אחר וכשאני אריץ אותו ב-sha1sum אני אקבל את אותו מספר – אז יכול להיות כל דבר זדוני במסמך הזה ואני לא אדע. זה אומר שכל הליך החתימות הדיגיטליות שנעשה ב-SHA-1 לא אמין.

וזה בדיוק מה שקרה. בשבוע האחרון חוקרים צרפתים וסינגפורים הוכיחו שהאלגוריתם SHA-1 פגיע להתקפה מסוג chosen-prefix collision attack ויותר חשוב: ההתקפה הזו זולה ובהישג ידם של ארגונים וחברות. מה זה אומר? זה אומר שהחוקרים יכולים, באמצעות מניפולציה, לגרום לכל מסמך שהוא להפיק מספר זיהוי גיבוב שזהה למסמכים אחרים.

בואו ונסביר בפשטות. אם למשל יצרתי תוכנה כלשהי ואני מעביר אותה ללקוח. יחד עם מספר הזיהוי המגובב שלה. הלקוח, כדי לוודא שאף אחד בדרך (כמו למשל האקר חובב פחמימות) לא הכניס בפנים קוד זדוני, יכניס את הקובץ של התוכנה לאותה פונקצית גיבוב. אם יצא לו אותו מספר – זה אותו קובץ שעזב את השרתים שלי.

אבל מה שהתוקפים עשו הוא, באמצעות מניפולציות שונות, לגרום לקבצים שונים לפי בחירתם להוציא אותו מספר זיהוי מגובב ייחודי! בידקו בעצמכם. הורידו את קובץ ה-PDF השני שהחוקרים סיפקו אם תבדקו אותו ב-sha1sum, תגלו שהוא נותו את אותו hash:

sha1sum shattered-2.pdf
38762cf7f55934b34d179ae6a4c80cadccbb7f0a *shattered-2.pdf

זה מסכן את כל מי שהסתמך על פונקצית הגיבוב SHA-1 לאבטחת קבצים. ויש לא מעט גופים כאלו ובראשם Github. כמובן שזה גם רלוונטי לתעודות אבטחה של אתרים, אבל כמעט שלא משתמשים באלגוריתם הזה.

כבר בשנת 2005 חוקרי אבטחה גילו חולשות תיאורטיות באלגוריתם הגיבוב SHA-1, אבל זו הפעם הראשונה שבוצעה התקפה מעשית.

זה לא אומר שהאקרים יוציאו לפועל את המתקפה הזו – אבל ברגע שהוכח שמתקפה כלשהי היא אפשרית – האקרים כבר מחממים מנועים ומתכנתים מכל העולם נדרשים לתקן את הקוד שלהם ולהחליף את פונקציות הגיבוב שבהם הם משתמשים. זה כאב ראש לא קטן שידרוש מאמצים רבים גם בתיקון הקוד וגם בתיקון בסיסי הנתונים – יש צורך בהחלפת כל מספרי הזיהוי המגובבים. מהלך שיש לו השפעה כלכלית לא מועטה על כל ארגון שהשתמש בזה. וכאמור יש רבים כאלו.

ארגונים שלא יתקנו את הקוד שלהם – ייפגעו יחד עם המשתמשים שלהם. כשהפגיעה יכולה להיות כלכלית ויכולה להיות גם פיזית במידה ומדובר במכשירי IoT. כרגע אין דרך ללקוחות הקצה לדעת או לפעול בעניין, אבל כאמור – האקינג זה לא משמים. והחולשות התיאורטיות של אתמול הופכות להתקפות תיאורטיות של היום והתקפות ממשיות של מחר. כרגע אין התקפות על בסיס החולשה של SHA-1. אבל יהיו. אם יש לכם קטעי קוד שמשתמשים ב-SHA-1. זה הזמן להשתמש באלטרנטיבות.