כדי להבין את המגבלות של בינה מלאכותית, חייבים להכיר אותה, גם באופן שטחי. ולהכרות באופן שטחי אין צורך בידע מתמטי מאד עמוק בפוסט הקצר הזה אני אסביר ואפילו אדגים בפשטות אלגוריתם של AI ואני חושב שהדרך הכי טובה להכיר AI כזה היא לנסות וליצור אחד כזה.
ראשית, רק לשם ההגדרה והנוחות – בינה מלאכותית (AI) זה מונח כללי של להביא את המחשב לחיקוי של בינה אנושית (או אפילו לא חיקוי, אפילו שאנחנו מאד רחוקים) – במסגרת השדה המאוד רחב של AI יש לנו למידת מכונה (ML) שזה נגזרת של השדה של AI. תפקיד למידת המכונה היא ללמוד נתונים כדי להבין אותם ולספק אותם לבינה המלאכותית.
זה נשמע תיאורטי אז בואו ונדגים עם משהו ממש קל – רגרסיה ליניארית. זה נשמע קצת מפחיד (אל תכנסו לערך בויקיפדיה אלא אם כן בא לכם לבכות). אבל אני אנסה להסביר את הבסיס כדי שנוכל להתקדם לעבר המטרה שלנו – בינה מלאכותית שאשכרה עושה משהו שאנחנו יכולים להבין. בגדול רגרסיה ליניארית מאפשרת לנו לקחת סט של נתון בלתי תלוי X ונתון שתלוי ב-X בשם Y ולמצוא את הקשר ביניהם.
למשל – נתון לא תלוי X הוא גודל הדירות בפתח תקווה. נתון שתלוי בגודל הדירה הוא המחיר שלה. ברור לנו שככל שגודל הדירה עולה, כך גם המחיר עולה. כלומר סוג של קו ישר (זה התרגום של ליניארי).
דוגמה נוספת של קשר ליניארי הוא הקשר בין גיל (משתנה לא תלוי, נכנה אותו X) למשכורת במגזר הציבורי (משתנה תלוי, נכנה אותו Y). אנחנו יודעים שככל שהותק עולה, כך גם המשכורת עולה.
אבל בכמה? בדרך כלל קו ליניארי מתואר באופן מתמטי כך:
y = a * x + bאם למשל אני אומר לכם שהמשוואה הליניארית של מחירי הדיור בפתח תקווה היא:
y = 10000 * x + 500000כאשר המשתנה הבלתי תלוי x הוא מ״ר של הדירה ו-y הוא המשתנה התלוי מחיר הדירה בש״ח – תוכלו להעריך כמעט בוודאות את מחירי הדיור בפתח תקווה. מה מחיר דירה שגודלה 100 מ״ר?
y = 10000 * 100 + 500000מחיר הדירה יהיה מיליון וחצי ש״ח: 1500000.
אם ננסה לשים את זה בגרף – זה יראה כך: הנקודות הכחולות הם מחירים של דירות אקראיות והקו האדום הוא המשוואה שאותה נתתי.
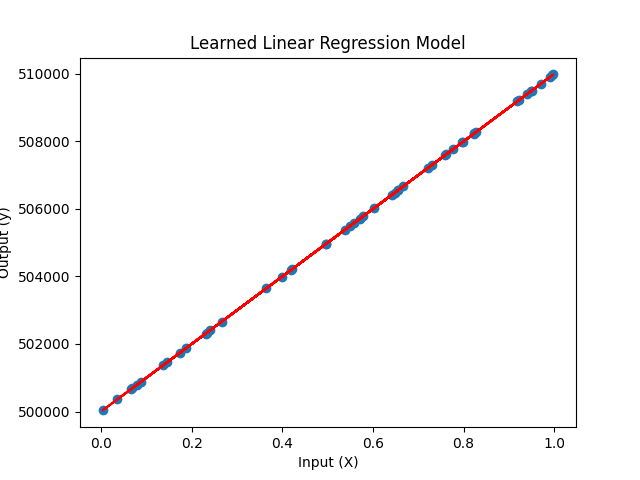
ה-a של המשוואה הוא השיפוע וה-b הוא הערך שלה אם ה-x הוא 0. כלומר נקודת החיתוך.
אבל החיים הם לא משוואה פשוטה. במקור יש לנו שונות ולפעמים דרמטית. אם אני אסתכל על מחירי דירות בפתח תקווה, אני אראה משהו כזה:
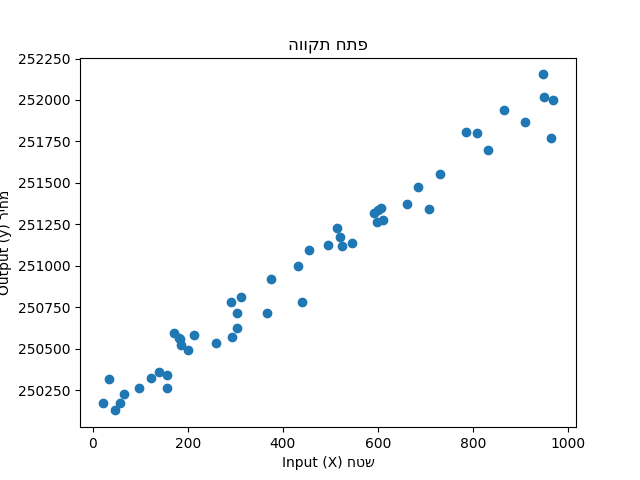
למה המחירים נראים ככה? כי זה העולם האמיתי, אבל עדיין אפשר לנסות למתוח איזשהו קו שיהיה מספיק קרוב לכל הנקודות. אפשר ליטרלי לחשב אותו מתמטית באופן כזה שה-m יהיה האופטימלי, זה שיהיה בו את הקירוב הטוב ביותר למציאות.
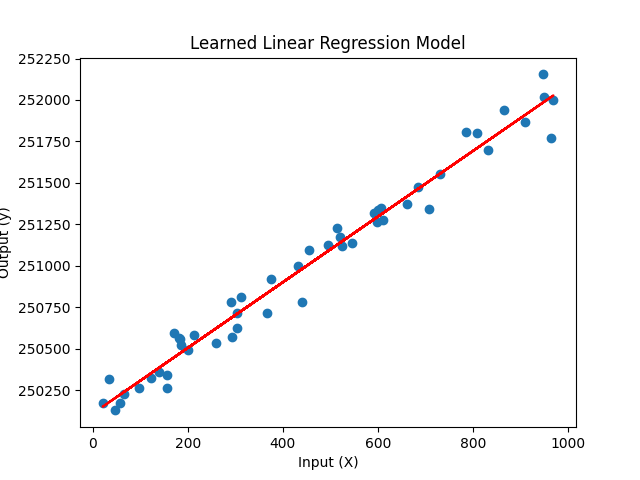
ברגע שיש לי את הקו, אני יכול לנחש את הנתונים העתידיים. החישוב הידני הוא מעניין אבל אני לא נכנס אליו פה. יש פה מאמר נפלא בעברית שמסביר את זה בצורה ממש מוצלחת לטעמי.
אני לא רוצה לעבוד קשה מדי – למה לא לתת למחשב לעשות את זה? הפעולה הזו נקראת למידת מכונה. כלומר אני מאכיל את המחשב בכל המידע שידוע לי על מחירי הדירות בפתח תקווה והוא מחשב את הרגרסיה בעצמו. העברת הנתונים נקראת ״אימון״ אחרי שאני מאמן את המחשב יש לי בעצם משוואה. המשוואה היא ה-m – השיפוע ו-b שידוע באנגלית כ intercept או bias.
ברגע שיש לי את המשוואה, אני יכול לבצע תחזית. ייתכן שהתחזית תיקלע, ייתכן שלא – אבל זו התחזית היחידה שאני יכול לעשות על פי הנתונים שיש לי כבר ותחזית לא פחות טובה מכל אדם שאני נותן לו את הנתונים האלו (בלי נתונים נוספים). זה בדיוק AI. לא בדיוק הכוכבים והזיקוקים שציפינו. לא?
טוב, בוא נעבור למעט קוד. הקוד הוא בפייתון כי בפייתון יש לנו מודול מוצלח בשם sklearn. יש לו גם גרסה ב-Node.js אבל אני אסביר בפייתון ואני מקווה שאנשי הג׳אווהסקריפט יזרמו.
ראשית צריך מידע. אני אצור מידע עם numpy באופן הזה:
import numpy as np
# Generate synthetic training data
np.random.seed(42)
X = np.random.rand(50, 1) # 50 random input data points
X = np.multiply(X, 1000)
y = 2 * X + 100 + 100 * np.random.randn(50, 1) + 250000 # output data points with some noise
אין פה איזה מדע טילים. בגדול אני יוצר X שהוא גודל הדירות ו-y שהוא המחיר. אני יוצר קצת רעש ורנדומליות כדי לדמות מחירים של השוק החופשי. יש לי בגדול שני מערכים – x ו-y. עכשיו צריך לאמן את המודל. איך? פה נכנס sklearn.linear_model שמאפשר לי לבצע אימון לפי המידע שיש.
import numpy as np
from sklearn.linear_model import LinearRegression
# Generate synthetic training data
np.random.seed(42)
X = np.random.rand(50, 1) # 50 random input data points
X = np.multiply(X, 1000)
y = 2 * X + 100 + 100 * np.random.randn(50, 1) + 250000 # output data points with some noise
# Train a linear regression model
model = LinearRegression()
model.fit(X, y)
אחרי האימון – יש לי בעצם את המשוואה. אני ליטרלי יכול לבקש מ sklearn להציג אותה:
# Display the learned model parameters (slope AKA m and intercept AKA bias)
slope = model.coef_[0][0]
intercept = model.intercept_[0] # bias
print(f"Slope: {slope:.2f}")
print(f"Intercept: {intercept:.2f}")ואני יכול כמובן לבצע תחזית לפי X אחרים.
X_test = np.array([[1500], [1750], [2000]]) # new input values
y_pred = model.predict(X_test) # predicted output values
print(f"X values: {X_test.flatten()}")
print(f"Predicted Y values: {y_pred.flatten()}")אם מישהו הגיע עד הסוף – אז תודו שזה לא הדבר הכי מורכב שיש. נכון, המתמטיקה מאחורי חישוב המשוואה היא מעט מורכבת (גם לא ממש – ברגע שמבינים מה המטרה) אבל בגדול sklearn מאפשרת לי לדלג באלגנטיות מעל השלב הזה של החישובים של עצמי.
הנה הקוד המלא, כולל הדפסה לגרפים נחמדים. אל תשכחו להתקין באמצעות פואטרי את numpy, scikit-learn ואת matplotlib.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# Generate synthetic training data
np.random.seed(42)
X = np.random.rand(50, 1) # 50 random input data points
X = np.multiply(X, 1000)
y = 2 * X + 100 + 100 * np.random.randn(50, 1) + 250000 # output data points with some noise
# Plot the training data
plt.scatter(X, y)
plt.xlabel("Input (X) חטש")
plt.ylabel("Output (y) ריחמ")
plt.title("הווקת חתפ")
plt.show()
# Train a linear regression model
model = LinearRegression()
model.fit(X, y)
# Display the learned model parameters (slope and intercept AKA bias)
slope = model.coef_[0][0]
intercept = model.intercept_[0] # bias
print(f"Slope: {slope:.2f}")
print(f"Intercept: {intercept:.2f}")
# Construct the regression equation
equation = f"y = {slope:.2f}x + {intercept:.2f}"
print("Regression equation: ", equation)
# Display the learned model parameters (slope and intercept)
print(f"Slope: {model.coef_[0][0]:.2f}")
print(f"Intercept: {model.intercept_[0]:.2f}")
# Visualize the learned model
plt.scatter(X, y)
plt.plot(X, model.predict(X), color="red")
plt.xlabel("Input (X)")
plt.ylabel("Output (y)")
plt.title("Learned Linear Regression Model")
plt.show()
X_test = np.array([[1500], [1750], [2000]]) # new input values
y_pred = model.predict(X_test) # predicted output values
print(f"X values: {X_test.flatten()}")
print(f"Predicted Y values: {y_pred.flatten()}")מבחינה מעשית כמובן שברגע שיש לנו נתונים שיכולים להתכנס לרגרסיה ליניארית אנחנו יכולים להפעיל את האלגוריתם הזה. למשל מכירות והוצאות פרסום, עלות מכר מול ייצור ואפילו משקעים ועננים. הקלות של השימוש באלגוריתם באמת מאפשרת למידת מכונה נאה.
כאן כמובן שזה קוד מאד פשוט. אם יש לנו הרבה מידע שאנחנו צריכים לחלץ ממנו את קו הריגרסיה, יכול להיות שנצטרך לפרק את המשימה הזו או להכניס את המידע הזה לתוך מסד נתונים. אבל בשביל Hello World הקוד הזה לגמרי בסדר.
לא מעט מתכנתים (גם אני) נרתעים קצת מעולם ה-AI וחבל. נכון, כשצוללים עמוק המתמטיקה מורכבת ממש וכמובן שזה רק גירוד של פני השטח, אבל בינה מלאכותית, גם GPT, היא מורכבת ומסובכת אבל היא לא אנושית וברגע שלומדים עליה ומתחילים לממש אותה, הפחד קצת נעלם. אני מקווה שהפוסט קצת עשה די-מיסטיפקציה לנושא הזה. אני בכל מקרה נהניתי לכתוב אותו ולעסוק בנושא.





8 תגובות
פוסט היכרות מצוין למי שלא מכיר את התחום.
כדאי להזכיר את העניין של overfitting והפרדת נתוני train מנתוני test. מי שנכנס ל ML בלי זה משול למי שלמד לרכוב על אופניים אבל עדיין לא למד להשתמש בברקס.
אני בהחלט שוקל מאמר המשך. המון תודה על הרעיון! 🙏
משהו קצת חסר לי.. הסברת נתון סטטיסטי שבני אדם משתמשים בו והראית איך עושים את זה בשורה אחת של קוד, אבל אין שום הסבר מה קורה מאחורה…
אה, שמתי קישור למאמר שמסביר את חישוב הרגרסיה. אני שם אותו שוב פה:
https://www.ai-blog.co.il/wp-content/uploads/2020/05/Machine-Learning-gadi-herman-Chapter-6.pdf
בגדול הרקע התיאורטי מאד מאד מעניין, אבל במקרה הזה דווקא התמקדתי בלהראות שהשד, לפחות ממבט ראשוני, לא נורא כל כך 🙂
יש איזה יתרון ב רגרסיה לינארית על פני polyfit מסדר ראשון של numpy? אני חושש שהאחרון עושה בשקט בשקט את אותה הפעולה בדיוק ולא מקבל קרדיט
הרעיון במודלים הוא שהכל שהמודל שמצליח להסביר משהו הוא יותר פשוט כך הוא כנראה יותר נכון. מודלים זו אמנות.
אם רגרסיה פשוטה זה Ai
אתם יכולים לשלוח לי הצעת עבודה אני יודע לעשות דברים יותר מעניינים מזה.
0526626467
כלכלן + אקטואר שלא משלמים לו מספיק
מאמר מעולה (אם כי אני לא מכיר node.js)
שאלה: ואם זה לא בפתח תקווה??