בפוסט הקודם למדנו על מספרים בינאריים בקוד. איך סופרים בבינארית, איך מספרים בשיטה הבינארית מוצגים בשפות כמו פייתון וג׳אווהסקריפט וגם על פעולות בינאריות שנקראות Bitwise operators כן למה זה חשוב ולמה כל מתכנת, גם כזה שעוסק בווב למשל, צריך להכיר מספרים בינאריים. בפוסט הזה אני מפרט על סוגים אחרים של Bitwise operators. למדנו קודם על &, | ו ^ ובפוסט הזה נכנס יותר עמוק לאופרטורים הנוספים שיש: NOT והשיפטים. אם לא קראתם את המאמר הקודם, כדאי לקרוא אותו.
BITWISE OPERATOR: ~ NOT
האופרטור הזה על הנייר הוא פשוט למדי. הוא עובד באופן הזה – הופך את המספר לשלילי ומעלה אותו באחד. אני אדגים:
~0b0101 = -0b110אופן החישוב הוא פשוט: 0101 הופך למינוס ואז מוסיפים לו אחד בבינארית והתוצאה היא 0110. בגדול, זה הופך מחמש למינוס 6. זו הנוסחה. כשאני עושה את זה למספר שהוא מינוס, אני מוריד אחד בבינארית ומסיר את המינוס.
~-0b110 = 0b0101למה זה שימושי? רואים את זה דווקא ב-low level יותר של ספריות עיבוד גרפיות וכמובן קריפטוגרפיה וכאשר צריך לבצע חישוב מספרים גדולים ממש באופן יעיל יותר. אני אראה דוגמת קוד קטנה ומובנת בפייתון (גם מתכנתי ג׳אווהסקריפט וכל שפה אחרת יוכלו להבין את זה בקלות כמובן)
# Define colors as 24-bit binary values (RRRRRRRRGGGGGGGGBBBBBBBB)
red = 0b111111110000000000000000
green = 0b000000001111111100000000
blue = 0b000000000000000011111111
# Function to invert colors using bitwise NOT operator
def invert_color(color):
return ~color & 0xFFFFFF
# Test the color inversion function
inverted_red = invert_color(red)
inverted_green = invert_color(green)
inverted_blue = invert_color(blue)
print("Inverted red:", format(inverted_red, '024b'))
print("Inverted green:", format(inverted_green, '024b'))
print("Inverted blue:", format(inverted_blue, '024b'))
זו דוגמה לא נורא מציאותית אבל אפשר בהחלט למצוא אותה בספריות שעושות עיבוד גרפי. אנו משתמשים אגב ב-AND bitwise אופרטור כדי לשמור על הערכים בתחום של 24 הביטים. אפשר להסיר אותם אגב.
בגדול, אם מספיק לכם להבין מה NOT עושה – כלומר מוסיפה מינוס ומוסיפה 1 לערך הבינארי או (אם המספר שלילי) מעלימה את המינוס ומורידה 1 מהערך הבינארי, אז סבבה. אבל אם אתם רוצים להעמיק קצת יותר – ובמיוחד להבין למה מורידים או מעלים 1 לערך הבינארי, אז אני אסביר בחלק הזה אבל אפשר לדלג לאופרטור הבא למי שלא רוצה להעמיק.
למה NOT מתנהג ככה? איך הוא באמת עובד?
הבסיס בהבנה של האופרטור NOT הוא להבין שמדובר בפעולה משלימה (באנגלית complement) ברמת הביטים.
על מנת להבין איך NOT עובדת ולמה מוסיפים את הביט הנוסף צריך להבין איך מספרים נראים באופן בינארי ב-low level. בינארי אנחנו יודעים. אבל איך מספרים באמת נראים? השאלה היא בכמה ביטים המערכת שלנו עובדת: 32 ביט? 64 ביט? בואו ונדגים עם 32 ביט איך נראה המספר חמש. בגדול בבינארי המספר חמש הוא 0101 אבל במערכת של 32 ביטים, כל מספר נמצא בתוך מערך של 32 ביטים שמחולק לשם הנוחות ל-4 ביטים:
0000 0000 0000 0000 0000 0000 0000 0101
מה כל האפסים האלו? אלו בלוקים ריקים. של 0. שלא מאוכלסים למספר כל כך קטן. אבל הביט השמאלי ביותר הוא חשוב, נקרא לו most significant bit או בראשי תבות MSB.
0000 0000 0000 0000 0000 0000 0000 0101
למה ה-MSB ובכלל כל הסיפור הזה של הביטים חשוב ל-NOT? ובכן, זה חשוב אם אנו רוצים לחשב מספר שלילי. למשל – איך אנחנו מציגים מספר שלישי בספירה בינארית? אז אנחנו משתמשים ב-NOT. ה-NOT הופך את כל הביטים מ-0 ל-1 והפוך. אם ניקח את המספר 5:
0000 0000 0000 0000 0000 0000 0000 0101 ונפעיל עליו NOT אז נקבל את התוצאה הזו – בעצם כל הביטים השתנו מ-0 ל-1 ונוסף 1:
1111 1111 1111 1111 1111 1111 1111 1010ה-MSB הוא 1. כלומר זה עכשיו המחשב יודע שמדובר במספר שלילי.
למה זה חשוב? כי בגלל ש-NOT הוא משלים – אז קל לנו להבין מה הערך של המספר החיובי. למשל אם אנחנו רוצים להציג את המספר לעין אנושית, אז בעצם כל מספר שה-MSB שלו הוא 1, עובר NOT ואז מוצג עם מינוס חביב.
כלומר, נניח והמחשב רוצה להציג מספר עבור המשתמש. הוא רואה שמדובר ב
1111 1111 1111 1111 1111 1111 1111 1010הוא מפעיל את NOT על המספר הזה. כלומר ממיר את כל הביטים להפכים ומוריד ביט אחד. מה יצא? מינוס 5:
0000 0000 0000 0000 0000 0000 0000 0101 בעצם הפעולה של הוספת ה-1 גורמת לפעולה ה-NOT להיות משלימה – אפשר לעשות אותה על המספר שוב ושוב ולקבל את אותה תוצאה.
על מנת לנסות להסביר למה הוספת ה-1, בואו ננסה לעשות את אותה פעולה בלי להוסיף או להסיר ביט אחד. הפעם במערכת של 4 ביטים. אם אני אקח את 0101 ואעשה לו היפוך ביטים. מה יצא? 1010 שזה מינוס שתיים וזה רחוק מ-5, שזו התוצאה המשלימה.
BITWISE OPERATOR: << left shift
האופרטור הזה בעצם מזיז את כל הביטים שמאלה לפי המספר שאנו נותנים לו ומוסיף 00 כמספר הפעמים למספר הבינארי. למשל, התוצאה של הפעלת left shift בערך של 2 על 0b0101 תגרום להוספת שני הביטים האחרונים:
0b0101 << 2 # 0b010100בעוד שקל להבין את האופרטור הזה, נשאלת השאלה למה בעצם צריך אותו. הוא חשוב אם זוכרים שבעצם הוא חישוב מתמטי קל – שימוש בו הוא כמו הכפלה ב-2 בחזקת המספר שנתנו לו.
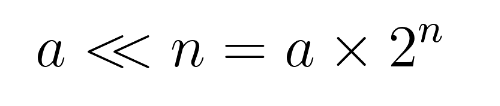
למשל, המספר 5 שהוא בבינארית 0b0101. אם אני אפעיל את left shift עליו:
0b0101 << 2התוצאה תהיה בבינארית 0b010100 שזה 20. שזה בדיוק כמו חמש כפול 2 בחזקת 2. אם אני אעשה את התרגיל הזה:
0b0101 << 3אני אקבל מספר בינארי של 0b0101000 שזה, כמה נוח 40. שזה בדיוק חמש כפול 2 בחזקת שלוש.
BITWISE OPERATOR: >> right shift
האופרטור right shift הוא בדיוק הפוך – הוא מוריד ביטים מהמספר הבינארי לפי המספר שנותנים לו. גם הוא די פשוט להבנה. אם אני משתמש בו עם הערך 2 במספר 01011, המספר החדש שיווצר יהיה 010. כלומר מ-11 ל-2.
0b01011 >> 2 = 0b010דוגמה טובה היא לשימוש בו היא המרות של מספרים. הנה למשל קוד שממיר ביטים לפורמטים שונים בפייתון:
def bytes_to_kilobytes(bytes):
return bytes >> 10
def bytes_to_megabytes(bytes):
return bytes >> 20
def bytes_to_gigabytes(bytes):
return bytes >> 30
# Test the conversion functions
file_size_bytes = 1073741824 # 1 GiB in bytes
file_size_kilobytes = bytes_to_kilobytes(file_size_bytes)
file_size_megabytes = bytes_to_megabytes(file_size_bytes)
file_size_gigabytes = bytes_to_gigabytes(file_size_bytes)
print("File size in bytes:", file_size_bytes)
# File size in bytes: 1073741824
print("File size in kilobytes:", file_size_kilobytes)
# File size in kilobytes: 1048576
print("File size in megabytes:", file_size_megabytes)
# File size in megabytes: 1024
print("File size in gigabytes:", file_size_gigabytes)
# File size in gigabytes: 1
ואם רוצים דוגמה בג׳אווהסקריפט – הנה למשל סקריפט קטן שמחשב את השורש של מספר מ-0 ועד 15.
function square(number) {
if (number < 0 || number > 15) {
throw new Error("Number must be between 0 and 15");
}
return (number << 1) + number;
}
// Test the square function
var input = 4;
var result = square(input);
console.log("The square of", input, "is", result);אפשר כמובן לשלב את שני השיפטים – והנה למשל דוגמה מאד מעשית של הורדה של איכות תמונה. אני משתמש בספריה הפייתונית Pillow כדי להוריד את איכות התמונה. איך אני מוריד את איכות התמונה? אני מוסיף קודם כל עם right shift ביטים ואז מוריד מהצד השני באמצעות left shift. זה מביא אותנו בעצם לא לדחיסה אבל לאובדן מידע.
from PIL import Image
def reduce_color_depth(image, bits):
factor = 8 - bits
for i in range(image.size[0]):
for j in range(image.size[1]):
r, g, b = image.getpixel((i, j))
r = (r >> factor) << factor
g = (g >> factor) << factor
b = (b >> factor) << factor
image.putpixel((i, j), (r, g, b))
# Load an image using the Pillow library
input_image = Image.open("input_image.jpg")
# Reduce the color depth of the image
reduce_color_depth(input_image, 4)
# Save the processed image
input_image.save("reduced_color_image.jpg")
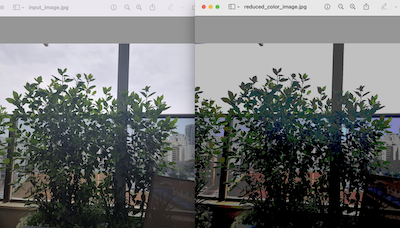
והנה ההבדל בין התמונות – השמאלית היא המקורית והימנית אחרי הפחתת הצבעים:
סיכום
גם במאמר הזה וגם במאמר הקודם למדנו על עבודה עם מידע בינארי. לא יוצא לנו לראות המון קוד שהוא bitwise ורובו נמצא בספריות שאנו צורכים. גם בניגוד לעבר, שימוש בו לא יביא דווקא אופטימיזציה לקוד (אולי על כך במאמר המשך). אבל בוודאות רואים אותו וכדאי לכל מתכנת להכיר אותו. בטח ובטח כאשר ניגשים לקוד שעושה אופטימיזציות וצריכים להבין מה הוא עושה.



2 תגובות
תודה רבה על כל התוכן!
אני חושב שיש טעות, הסקריפט של השורש לא נכון..
יש דרך פשוטה יותר להסביר איך ה-MSB "הופך סימן".
אסביר עם 4 ביט.
הביט הראשון ערכו 2 בחזקת אפס (ז.א. – 1 כאשר הוא מסומן).
הביט השני ערכו 2 בחזקת אחד (ז.א. – 2 כאשר הוא מסומן).
הביט השלישי ערכו 2 בחזקת שתיים (ז.א. – 4 כאשר הוא מסומן).
הביט הרביעי ערכו *מינוס* (2 בחזקת שלוש) (ז.א. – מינוס 8 כאשר הוא מסומן).
ההסבר הזה מאפשר גם להבין מדוע הטווח לא סימטרי לאפס 🙂